Overview

For 30 years, the Explorer’s Club of Pittsburgh has run a mountaineering school through the winter, guiding students in outings and exercises to build advanced skills for mountain climbing. Every student of the mountaineering school trains on the stairs of the University of Pittsburgh’s Cathedral of Learning. A typical training session consists of multiple repetitions up the Cathedral’s 34-story stairwell, carrying a weighted backpack to simulate real mountain ascents. I analyzed data from 10 years of training logs, including 129 students and 10,000+ repetitions of the stairs. From 2011-present, students’ climbing paces exhibited consistent response to heavier packs and footwear.

Descriptive Statistics

Number of seasons	10
Number of students	129
Number of reps	11,813
Reps per student, average	91.6
Number of workouts	1,667
Workouts per student, average	12.9
Number of workouts with recorded pack weights	1,659
Average pack weight, pounds	27
Number of workouts with recorded footwear	1,567
Average pace, minutes per rep	12.6
Fastest pace, minutes per rep	4.67
Slowest pace, minutes per rep	32

Figures

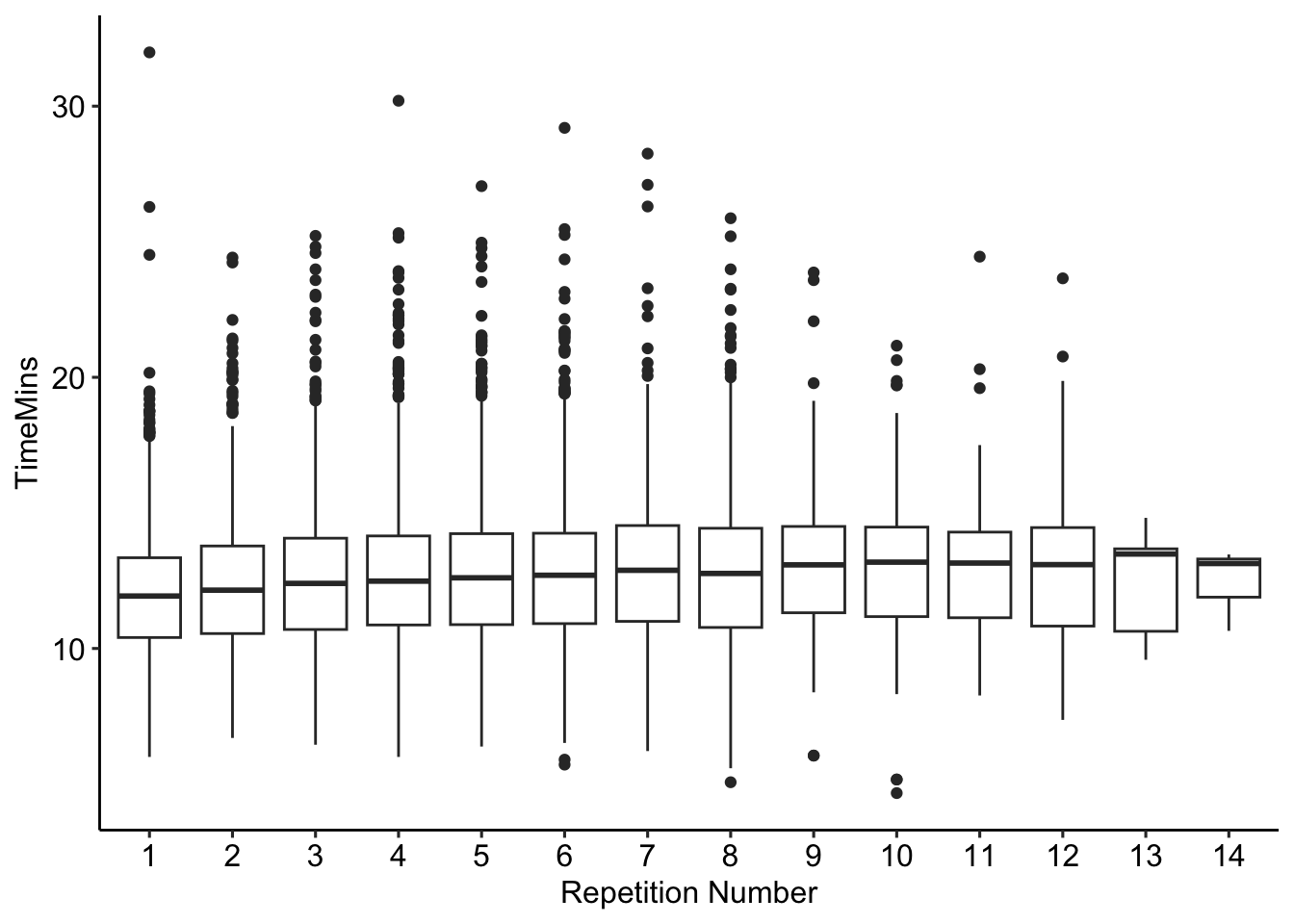
The following boxplot illustrates the typical pace per rep, across all students and workouts:

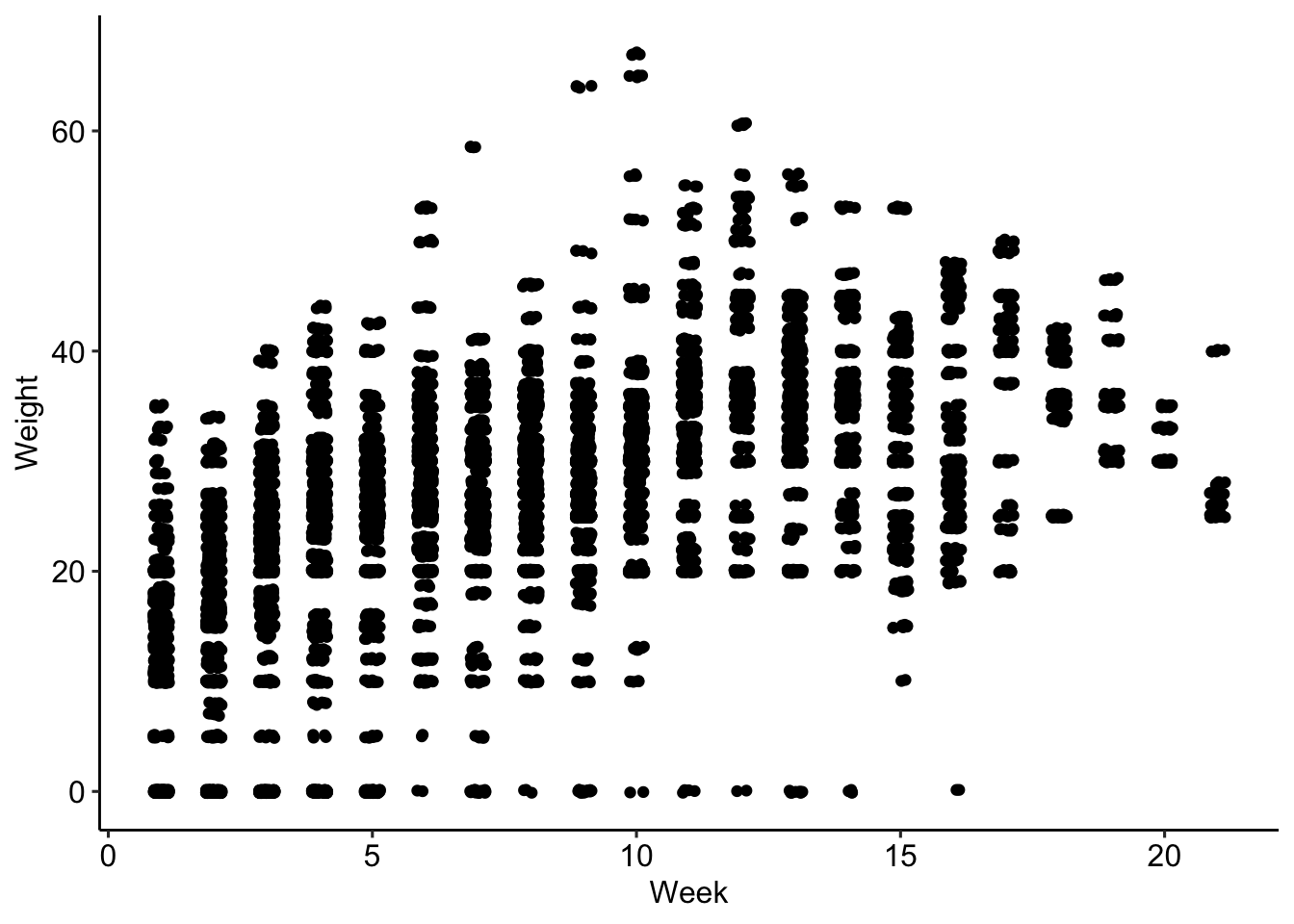
Across sequential reps, the average pace varied from 12 to 13.1 minutes.

Figure 1: Time (in minutes) taken to complete each rep of the stairs

The following scatterplot illustrates the typical pack weight by week of the season, across all years:

Pack weights tended to increase gradually throughout the season; however, there is a noticeable step-up in weights after Week 10.

Figure 2: Weight (in pounds) carried for each workout by week

Exploratory Analyses

Across all recorded reps and accounting for pack weight, I’m interested in the average difference between footwear types in terms of pace. The following footwear types were encoded numerically:

Running shoes
Hiking boots
Mountaineering boots

To estimate the difference in pace associated with footwear, I use linear regression. For reps \(i=1, ..., N\), I treat \(y_i\) as the pace (in minutes), \(x_i\) as the numerical index of footwear (in the list above), and \(z_i\) as pack weight (in pounds). Thus, we have:

\[ y_i=\alpha[x_i]+\beta z_i + \epsilon_i \] where \(\alpha[1],..., \alpha[3]\) and \(\beta\) are estimated via least-squares.

I fit the model and examine the regression coefficient summaries below:

Interpreting the regression coefficients, an additional five pounds of pack weight was associated with a slowdown in pace of 0.327 minutes; this equates to roughly 20 seconds per repetition. Accounting for pack weight, the difference between mountaineering boots and running shoes was a slowdown in pace of 1.35 minutes.

Table 1: Regression coefficients from least-squares estimation

Effect	Estimate (Mins)	95% CI
Footwear index
1	9.7	9.6, 9.9
2	11	10, 11
3	11	11, 11
Weight	0.07	0.06, 0.07
Abbreviation: CI = Confidence Interval

Discussion

Across the population of mountaineering school students, the average pace of climbing one rep of the Cathedral stairs was 12.6 minutes, with a vertcial elevation gain of about 132 meters per repetition.

Any rep measured in minutes is easily expressed as the number of meters climbed in one hour, assuming a constant pace. The formula for this conversion is below:

\[ \text{Meters per hour (mph)}=60\times \frac{132}{\text{Minutes per rep}} \]

The average pace for the students was 629 mph. A 2004 study of hikers found a typical climbing pace of 317 mph in the Austrian Alps, with variation between 180 and 480 mph. Thus, the typical climbing pace observed in this dataset was exceptionally fast by alpine standards, but also occurred in a controlled training environment near sea-level.

The study was published in Research in Sports Medicine, and titled “Exercise Capacity for Mountaineering: How Much Is Necessary?”, by Martin Burtscher.

Additionally, student climbing paces exhibited negative responses to heavier footwear and pack weights, as would be expected given the endurance aspect of the training exercise. Extrapolating from the regression results in Table 1, an increase in pack weight from 20 to 30 pounds would be expected to slow the average student by 42 seconds per rep. In climbing terms, this would potentially slow the pace from 629 to 595 mph.

One noteworthy limitation of this analysis is that the results demonstrate average tendencies; however, it is likely that students responded differently to increased loads. Therefore a revised analysis ought to account for student-level heterogeneity in the efefcts of footwear and packweight. A multi-level model via Bayesian methods would offer means to address this limitation.